AGE-MOEA: Adaptive Geometry Estimation based MOEA¶
AGE-MOEA [1] follows the general outline of NSGA-II but with a modified crowding distance formula. The non-dominated fronts are sorted using the non-dominated sorting procedure. Then the first front is used for normalization of the objective space and estimation of Pareto front geometry. The p parameter of a Minkowski p-norm is estimated using the closest solution from the middle of the first front. The p-norm is then used to compute a survival score that
combines distance from the neighbors and proximity to the ideal point.
AGE-MOEA uses a binary tournament mating selection to increase some selection pressure. Each individual is first compared using the rank and then the computed score that represent both proximity and spread.
Example¶
[1]:
from pymoo.algorithms.moo.age import AGEMOEA
from pymoo.factory import get_problem
from pymoo.optimize import minimize
from pymoo.visualization.scatter import Scatter
problem = get_problem("zdt1")
algorithm = AGEMOEA(pop_size=100)
res = minimize(problem,
algorithm,
('n_gen', 200),
seed=1,
verbose=False)
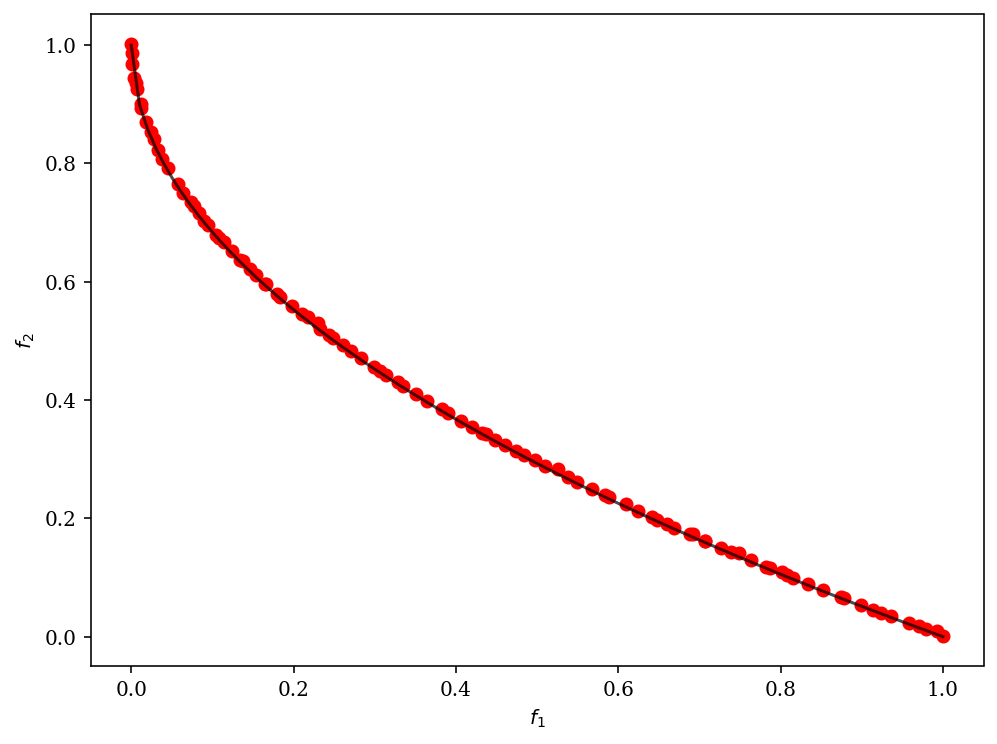
plot = Scatter()
plot.add(problem.pareto_front(), plot_type="line", color="black", alpha=0.7)
plot.add(res.F, color="red")
plot.show()
[1]:
<pymoo.visualization.scatter.Scatter at 0x7f017aa630d0>
Moreover, we can customize AGE-MOEA to solve a problem with binary decision variables, for example, ZDT5.
[2]:
from pymoo.algorithms.moo.age import AGEMOEA
from pymoo.factory import get_problem, get_sampling, get_crossover, get_mutation
from pymoo.optimize import minimize
from pymoo.visualization.scatter import Scatter
problem = get_problem("zdt5")
algorithm = AGEMOEA(pop_size=100,
sampling=get_sampling("bin_random"),
crossover=get_crossover("bin_two_point"),
mutation=get_mutation("bin_bitflip"),
eliminate_duplicates=True)
res = minimize(problem,
algorithm,
('n_gen', 500),
seed=1,
verbose=False)
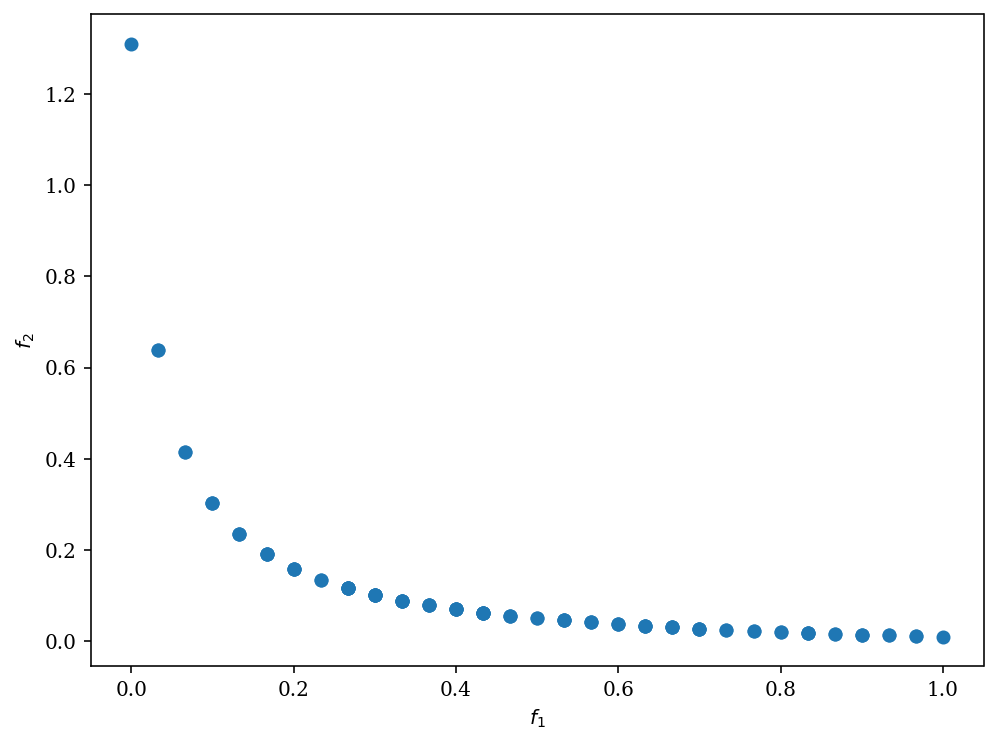
Scatter().add(res.F).show()
[2]:
<pymoo.visualization.scatter.Scatter at 0x7f01789607f0>
This algorithm is based on [1] and its Matlab implementation of the PlatEMO library. This Python version has been implemented by BenCrulis
API¶
-
class
pymoo.algorithms.moo.age.AGEMOEA(self, pop_size=100, sampling=FloatRandomSampling(), selection=TournamentSelection(func_comp=binary_tournament), crossover=SBX(eta=15, prob=0.9), mutation=PM(prob=None, eta=20), eliminate_duplicates=True, n_offsprings=None, display=MultiObjectiveDisplay(), **kwargs) Adapted from: Panichella, A. (2019). An adaptive evolutionary algorithm based on non-euclidean geometry for many-objective optimization. GECCO 2019 - Proceedings of the 2019 Genetic and Evolutionary Computation Conference, July, 595–603. https://doi.org/10.1145/3321707.3321839
- Parameters
- pop_sizeint
The population sized used by the algorithm.
- sampling
Sampling,Population,numpy.array The sampling process defines the initial set of solutions which are the starting point of the optimization algorithm. Here, you have three different options by passing
(i) A
Samplingimplementation which is an implementation of a random sampling method.(ii) A
Populationobject containing the variables to be evaluated initially OR already evaluated solutions (F needs to be set in this case).(iii) Pass a two dimensional
numpy.arraywith (n_individuals, n_var) which contains the variable space values for each individual.- selection
Selection This object defines the mating selection to be used. In an evolutionary algorithm each generation parents need to be selected to produce new offsprings using different recombination and mutation operators. Different strategies for selecting parents are possible e.g. selecting them just randomly, only in the neighborhood, using a tournament selection to introduce some selection pressure, …
- crossover
Crossover The crossover has the purpose of create offsprings during the evolution. After the mating selection the parents are passed to the crossover operator which will dependent on the implementation create a different number of offsprings.
- mutation
Mutation Some genetic algorithms rely only on the mutation operation. However, it has shown that increases the performance to perform a mutation after creating the offsprings through crossover as well. Usually the mutation operator needs to be initialized with a probability to be executed. Having a high probability of mutation will most of the time increase the diversity in the population.
- eliminate_duplicatesbool
The genetic algorithm implementation has a built in feature that eliminates duplicates after merging the parent and the offspring population. If there are duplicates with respect to the current population or in the offsprings itself they are removed and the mating process is repeated to fill up the offsprings until the desired number of unique offsprings is met.
- n_offspringsint (default: None)
Number of offspring that are created through mating. By default n_offsprings=None which sets the number of offsprings equal to the population size. By setting n_offsprings=1 a, so called, steady-state version of an algorithm can be achieved.
